Dan Batcheldor
PhD, Astrophysicist
Introduction
Over a period of a few hours, we see the moon move differently from the stars. Over a period of a few weeks, we see the sun doing something different, too. It rises and sets at different points on the horizon.
Wandering Stars
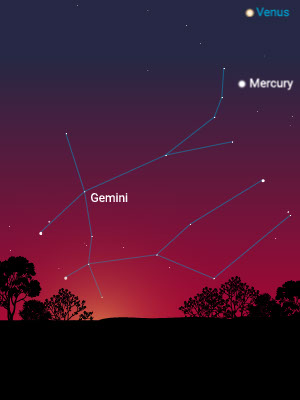
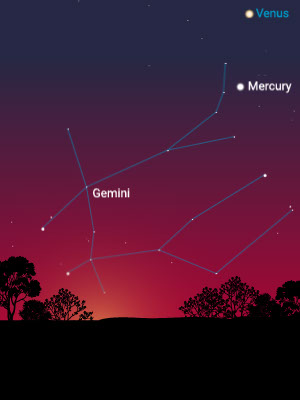
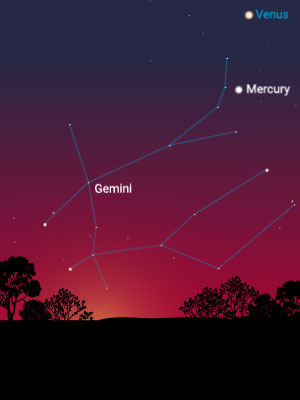
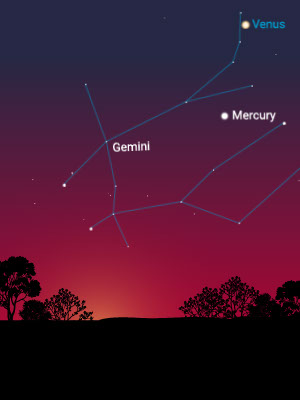
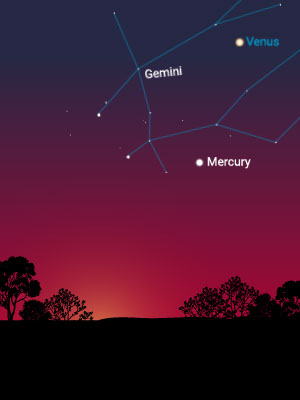
To the unaided eye, there are five wandering stars: the planets Mercury, Venus, Mars, Jupiter, and Saturn. In fact, the word “planet” means “wandering star.” When those five are combined with the sun and the moon, we end up with seven handy names for the days of the week.
Each visible planet moves with a different speed across the sky and through the constellations. Mercury passes through Gemini in about two weeks, Venus about three weeks, Mars about six weeks, Jupiter about three or four months, and Saturn six or seven months. The sun takes about four weeks due to the orbit of Earth.
Mercury and Venus go from one side of the sun to the other. Mars, Jupiter, and Saturn wiggle back and forth on the sky regularly performing retrograde pirouettes.
The Heliocentric Model
Then, over periods that are greater than a few weeks, it is easy to notice that some star-like objects wander in and out of the constellations. Some, from time to time, appear to move in a retrograde manner (i.e., backward in the sky).



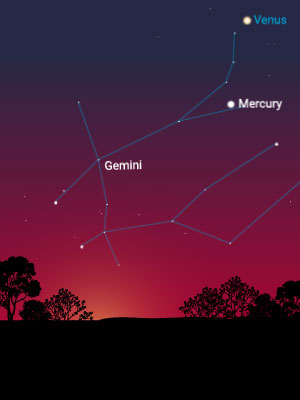
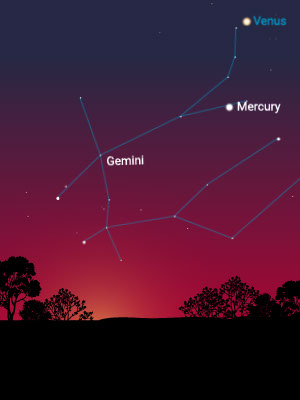
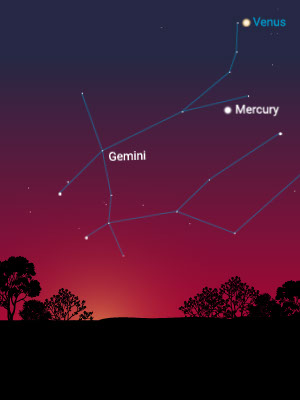
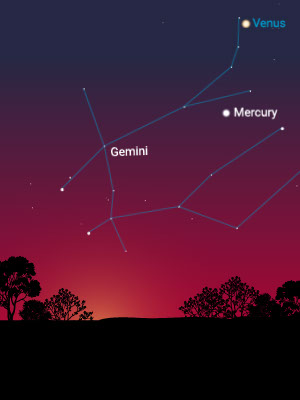
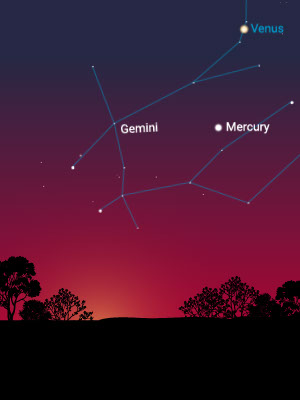
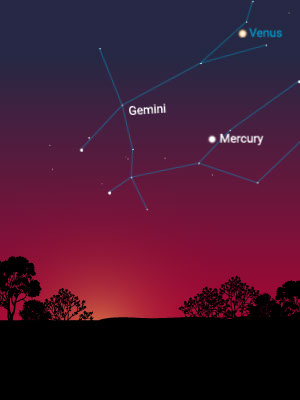
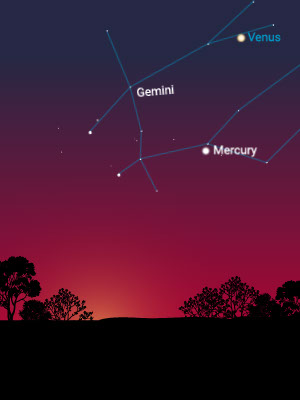
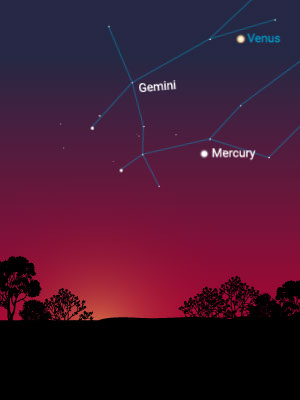
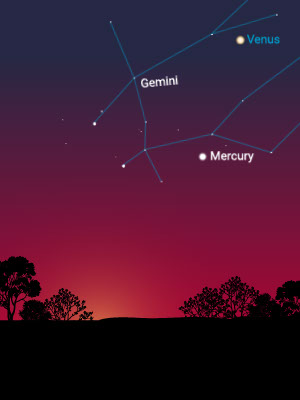
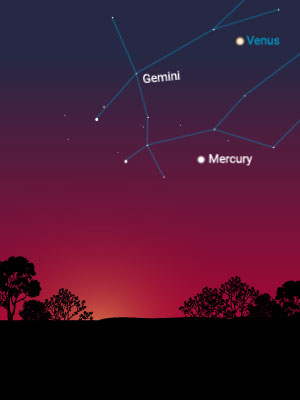
The Distance to the Sun
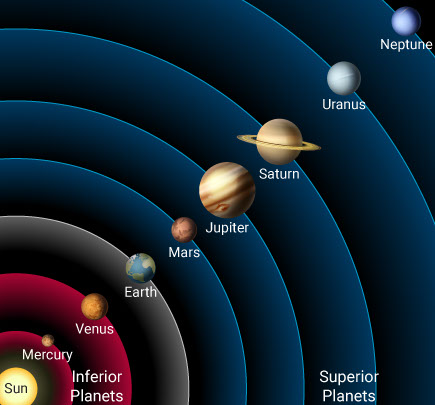
With this data, one can place the planets in their correct distance order from the sun and into the heliocentric model.
Mercury is fastest, appearing on one side of the sun and then the other. It is closest to the sun.
Venus does the same, but much more slowly, and it separates itself farther from the sun than Mercury does. It is second closest to the sun. Mercury and Venus are called “inferior” planets because they are closer to the sun than Earth is.
Based on the apparent motion of the sun, Earth comes next. This also provides an explanation for the retrograde motion of the three remaining planets. They are “superior” planets because they are farther from the sun than Earth is. The apparent backward motion of these planets happens when Earth overtakes them on its way around the sun.
Mars is the fastest of the superior planets, followed by Jupiter and then Saturn. It is their observed speeds across the sky that determines their distance from the sun. The farther away, the slower the observed speed. The other planets, Uranus and Neptune, cannot be seen without the aid of a telescope.
Calculating Relative Distances
Earth takes one year to complete a single lap around the sun, and we say its relative distance to the sun is 1 astronomical unit. But what is an astronomical unit in kilometers?
To answer this, we start by finding the relative distances and relative periods of the other planets as compared to Earth. Calculating the relative distances to Mercury and Venus once again relies on simple trigonometry because all we need to know is the largest angle each inner planet has with respect to the sun.
As an inner planet orbits around the sun, we see it get farther and farther away, stop, and then go back. We can measure the angle between the planet and the sun at the point where the planet appears to stop and simply take the sine of that angle. This would give us the distance of that planet in astronomical units.
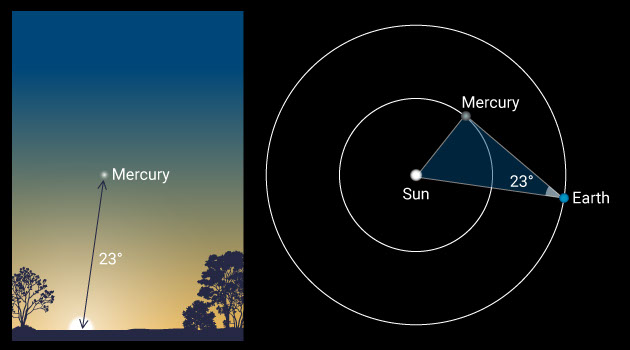
For Mercury, the angle is 23 degrees, on average, which makes the relative distance of Mercury from the sun about sin(23) = 0.39 astronomical units.
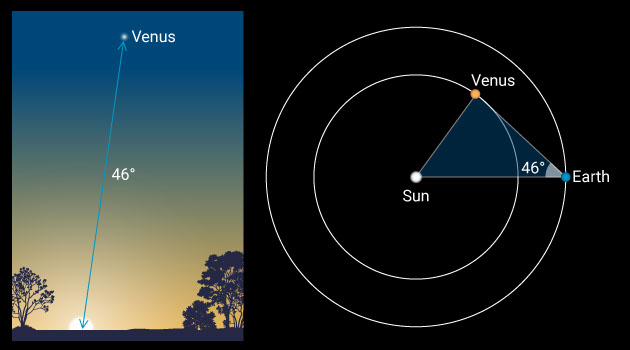
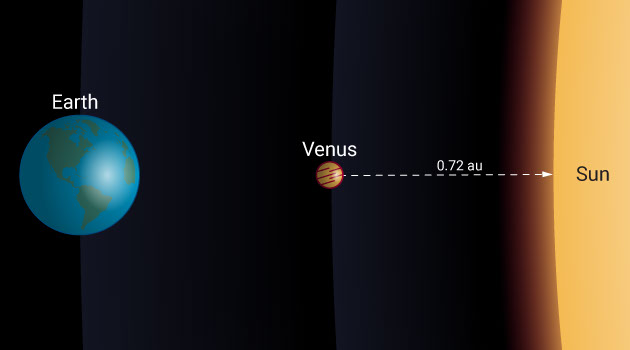
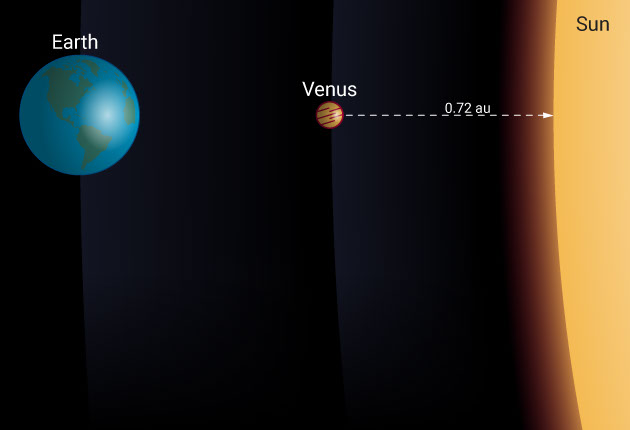
For Venus, the angle is about 46 degrees, giving a relative distance of sin(46) = 0.72 astronomical units.
These Venus and Mercury observations can be made without a telescope and with a lot of patience.
Parallax
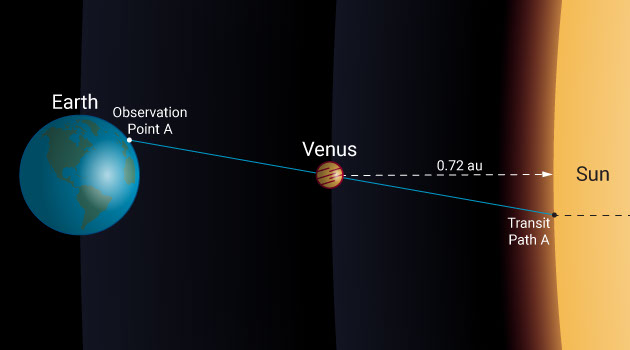
We can find the absolute distance to Venus using parallax as it passes in front of the sun, and then simply divide that distance by 0.72 (the number of astronomical units Venus is from the sun) to get the absolute distance of Earth from the sun.
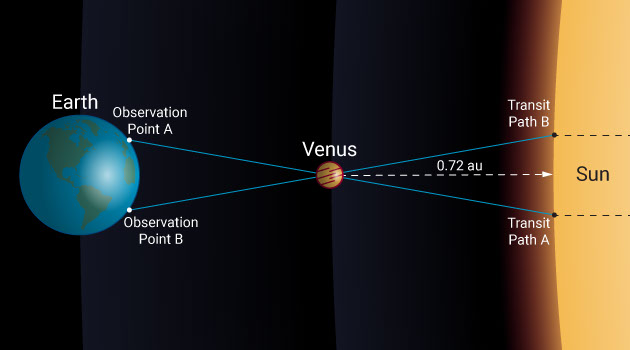
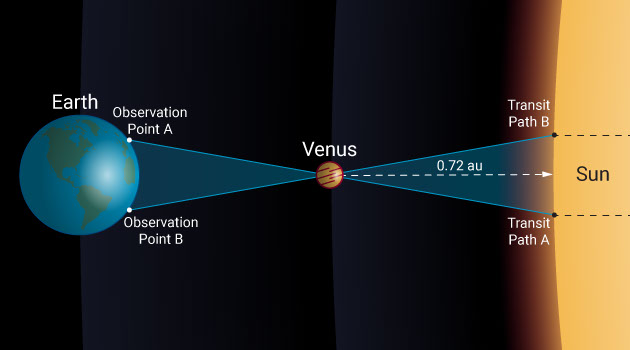
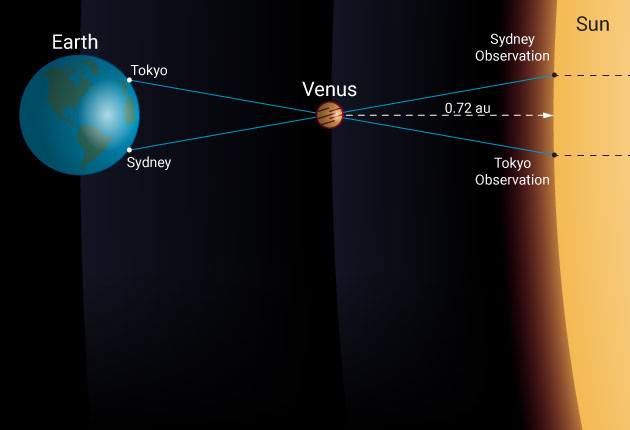
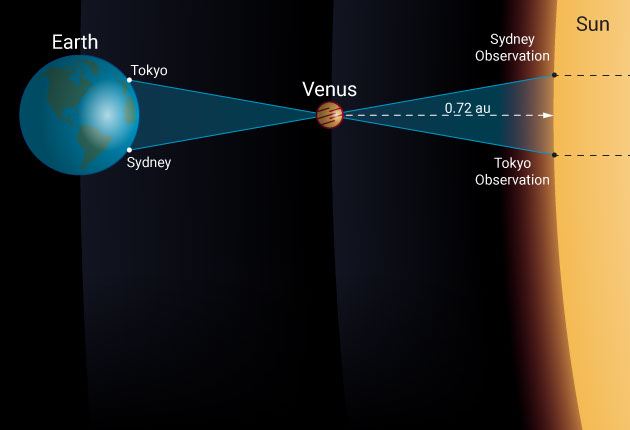
All we need to do is wait for Venus to pass in front of the sun and observe the event from two different places on Earth. These two places will form the base of our parallactic triangle from which the distance estimate can be made.
Parallax is the apparent shift in the position of an object against a background when observed from two different locations. You can easily replicate the effect by holding out a finger and winking your eyes back and forth. The closer your finger is, the bigger the apparent shift in position will be. Therefore, by measuring parallax from a known baseline, we can determine distance.

<
>
Due to the number of factors that can impact this calculation, students can expect a 3 percent margin of error.
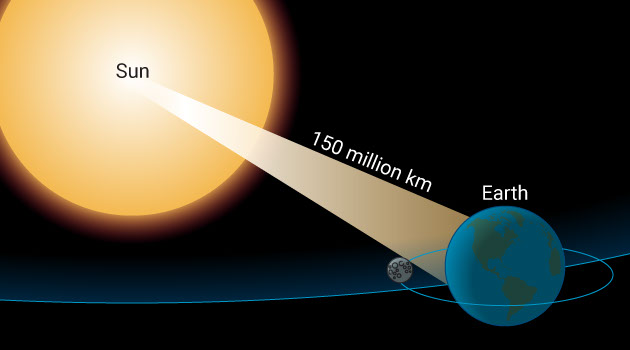
Despite all the difficulties with making such measurements, when the results of all the efforts made during the 18th and 19th century adventures were averaged, the distance estimates for the sun did indeed work out to about 150 million kilometers.
The Transit of Venus
The orbit of Venus is tilted by several degrees compared to that of Earth. This means that Venus can miss the 0.51 degree solar disc, making transit events quite rare.

Click on each title to learn more about the history behind Venus transit observations.
The 2012 Transit of Venus
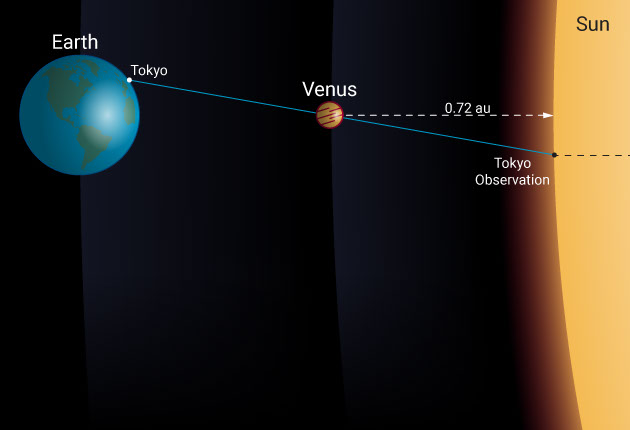
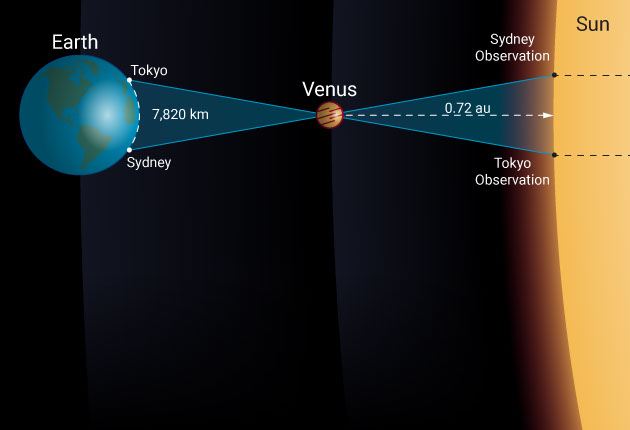
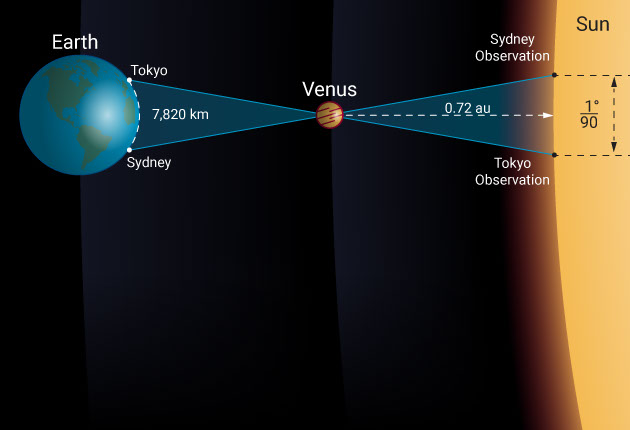
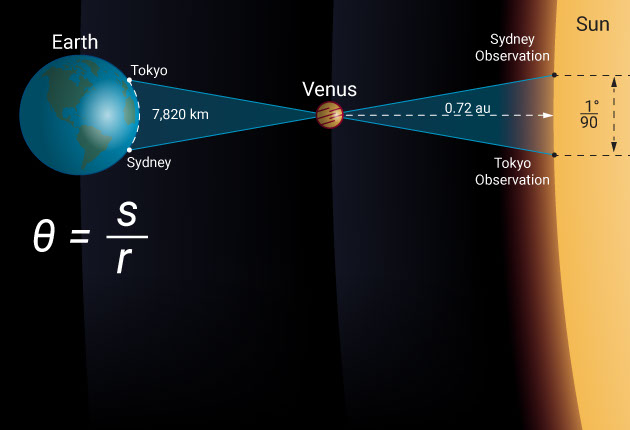
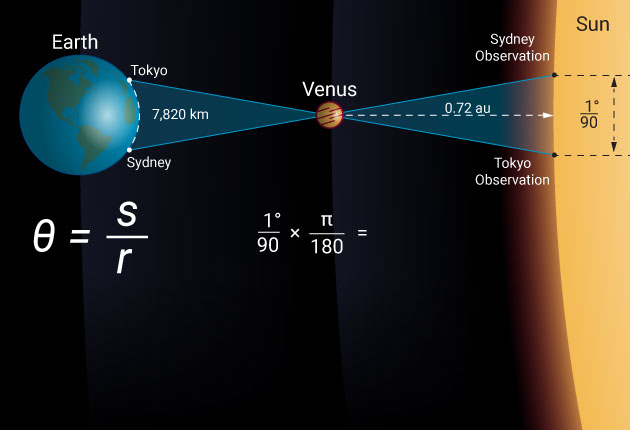
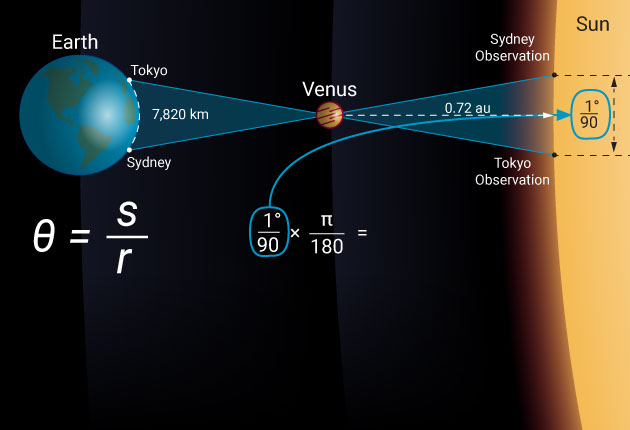
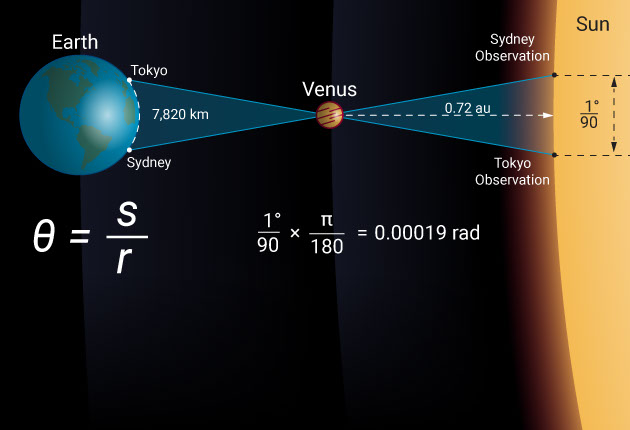
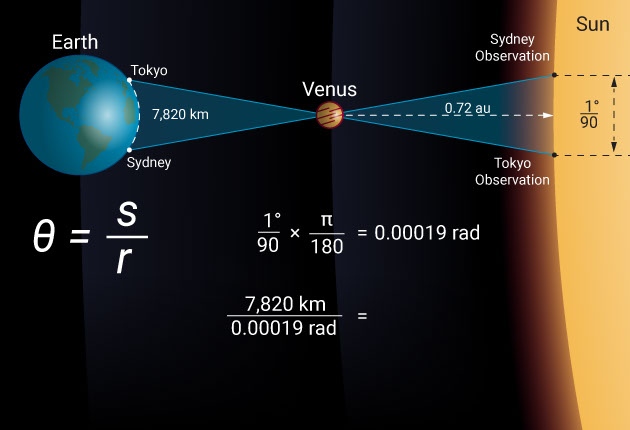
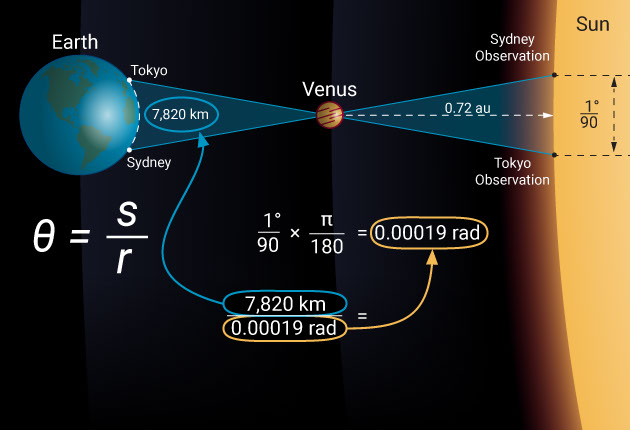
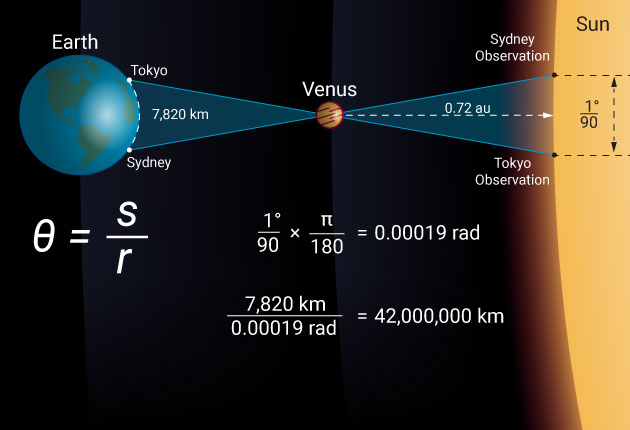
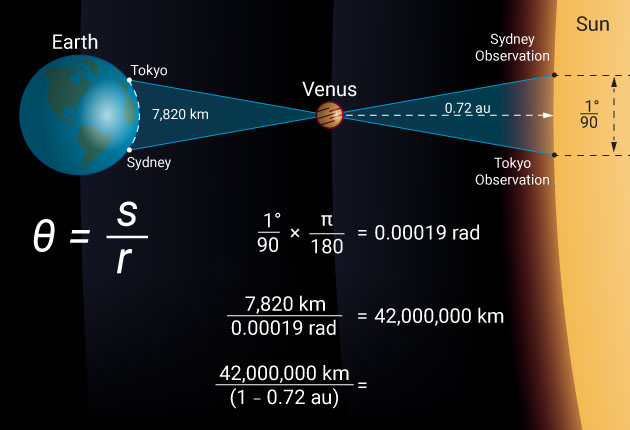
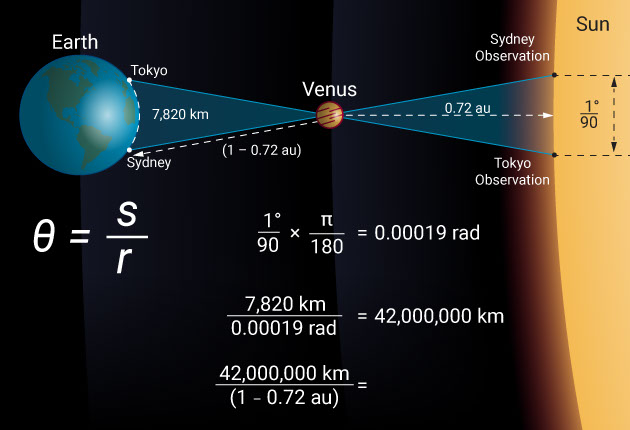
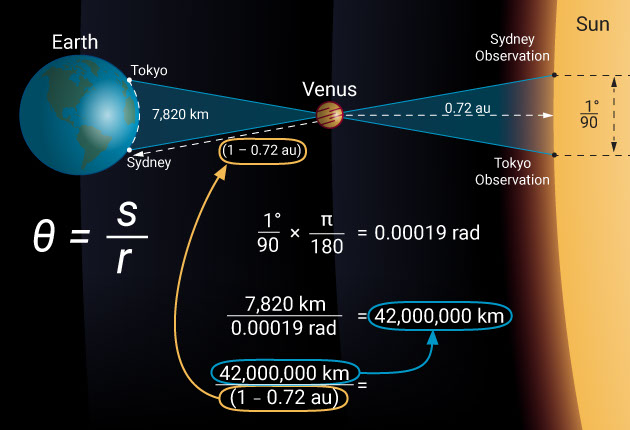
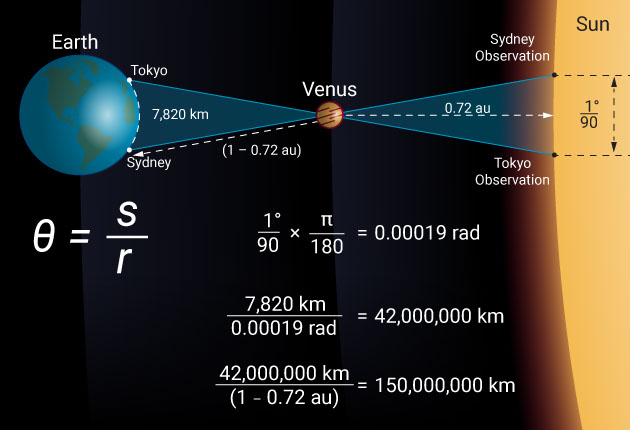
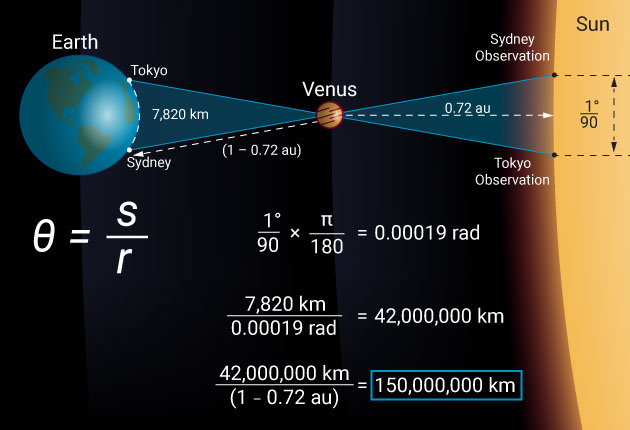
Let’s take the June 5th and 6th 2012 transit of Venus as an example and see what the difference was from two widely spaced observation locations like Sydney and Tokyo. In this case, the baseline is 7,820 kilometers. Observed from Tokyo, Venus passed across the disk of the sun 0.67 arcminutes, which is 1/90 of a degree closer to the solar equator than it did when observed from Sydney.
However, by simply remembering that θ = s / r, we find that the distance to Venus is 7,820 divided by 1/90 of a degree, which is 0.00019 radians. Venus is, therefore, at a distance of 42 million kilometers. When divided by the relative distance to Venus (1 – 0.72 au), this makes the distance to the sun a whopping 150 million kilometers.
![]() Johannes Kepler
Johannes Kepler
Based on the high precision of observations made by Tycho Brahe, Johannes Kepler (Brahe’s PhD student) was able to formulate three laws of planetary motion that allowed him to predict Venus transits in 1627 and 1631, with a follow-up near transit in 1639. Kepler was slightly off in his calculations, and the 1631 transit was just a near miss. In 1639, the transit of Venus was first observed.
![]() Major Investments
Major Investments
In the mid-17th century, the scientific, philosophical, and theological implications for determining the scale of the solar system and the astronomical unit, in particular, were very high. Consequently, major investments were made by multiple individuals and governments to observe and record the Venus transits predicted for 1761, 1769, 1874, and 1882 from the widest baselines possible.
![]() James Cook
James Cook
Global adventures, which were carried out by the likes of James Cook (1728–1779), had other merits, such as testing navigational methods and finding new land in partially mapped oceans.
![]() Edmond Halley
Edmond Halley
The parallactic Venus-sun transit method itself is quite simple and was realized by Edmond Halley (1656–1742). From two different observation points, Venus will appear to transit across two different segments of the solar disc. One path will be closer to the equator of the sun than the other, and so the parallactic angle can be determined.
Johannes Kepler
Major Investments
James Cook
Edmond Halley
<
>
We have now demonstrated how to determine the distance to the sun – the astronomical unit. An astronomical unit is an astronomical number, so it is no coincidence that the term “astronomical” is used as a metaphor for something really, really big or something really, really important.
NASAEarthObservatory. (2012, June 6). Venus transit (full disk) [Video file]. Retrieved November 14, 2016, from https://www.youtube.com/watch?v=jJ1CuczGwvk
Dunn, A. (2004, November 5). Newton’s telescope replica [photograph]. Retrieved December 19, 2016, from https://commons.wikimedia.org/wiki/File:NewtonsTelescopeReplica.jpg
